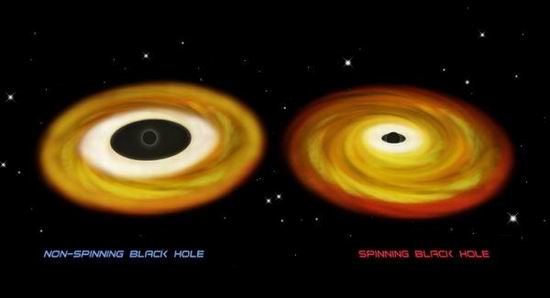
|
|
 |
|
 |
|
Вращающиеся черные дыры
 Рассмотренную нами шварцшильдовскую черную дыру нельзя считать реальным физическим объектом в строгом смысле этого слова. Дело в том, что если черные дыры действительно существуют, то они должны образовываться из вращающихся тел (т. е. из тел, обладающих собственным моментом импульса), и, кроме того, эти тела могут иметь отличный от нуля электрический заряд. Но если большинство объектов во Вселенной можно все же считать электрически нейтральными, то вращение—это общее свойство, присущее звездам, планетам и галактикам. Черная дыра, возникающая в результате коллапса вращающейся массивной звезды, сама должна вращаться вокруг своей оси с большой скоростью; ведь нам доподлинно известно, что нейтронные звезды являются быстро вращающимися объектами.
Теоретические исследования, проведенные Б. Картером, В. Израэлом, Д. Робинсоном и С. Хокингом, показали, что с точки зрения внешнего наблюдателя черные дыры могут иметь только три характеристики: свойства черной дыры полностью определяются ее массой М, электрическим зарядом Q и собственным моментом импульса J. Эти три характеристики должны остаться у черной дыры, поскольку они связаны с полями дальнодействующих сил, которые оказывают влияние на удаленные объекты. Гравитационное поле, величина которого зависит от массы М и момента импульса /, изменяется обратно пропорционально квадрату расстояния от источника; электромагнитная сила, обусловленная зарядом Q, ведет себя подобным же образом. При формировании черной дыры гравитационное поле вне горизонта событий продолжает воздействовать на распространение световых лучей и движение объектов с ненулевой массой покоя. Аналогично электромагнитное поле, связанное с полным электрическим зарядом черной дыры, также будет оказывать влияние на окружающие тела. Никакие другие свойства вещества, участвующего в формировании черной дыры, не передаются ей “в наследство”. Подчеркивая этот аспект природы черных дыр, профессор Дж. А. Уилер весьма остроумно заметил: “У черной дыры не может быть волос”. Иными словами, коллапсирующее тело быстро достигает состояния, единственными характеристиками которого являются масса, заряд и собственный момент импульса других отличительных черт у черной дыры нет.
Решение уравнений поля для сколлапсировавших массивных тел с электрическим зарядом и моментом импульса— чрезвычайно трудная задача. В 1916—1918 гг. X. Райсснер и Дж. Нордстрём нашли решение, описывающее черную дыру с массой М и электрическим зарядом Q, но лишь в 1963 г. австралийский математик Рой П. Керр получил решение уравнений поля для черной дыры с массой М и собственным моментом импульса J. Только после этого стало возможно построить достаточно реалистические модели черных дыр. Примерно через 2 года после Керра Э. Ньюмен с соавторами нашел решение, в котором фигурировали все три характеристики черных дыр: М, Q и J. Решения Керра Ньюмена, по-видимому, исчерпывают все возможные варианты моделей черных дыр.
Впрочем, вряд ли в природе есть черные дыры, несущие сколько-нибудь существенный электрический заряд, а если таковые и существуют, то недолго. Дыра, образовавшаяся из вещества с большим положительным электрическим зарядом, будет интенсивно притягивать оказавшиеся по соседству отрицательные заряды и отталкивать положительные. В результате через некоторое время первоначальный заряд черной дыры будет нейтрализован.
Что же касается вращающихся черных дыр, то они как внутри, так и вне горизонта событий обладают рядом замечательных свойств. Вне горизонта событий таких дыр простирается область, называемая эргосферой (рис. 34), которая снаружи ограничена некой поверхностью (разумеется, не твердой), именуемой пределом стационарности. Последний касается горизонта событий в двух точках — “полюсах” черной дыры. Внутри предела стационарности ничто не может оставаться в покое: даже если бы ваш космический корабль двигался с околосветовой скоростью, то в эргосфере вы бы не избежали вынужденного вращения—само пространство там как бы увлекается вращением черной дыры и закручивается вокруг ее оси. Космический корабль, попавший внутрь эргосферы, в принципе, может ее покинуть, для этого достаточно, включив двигатели, направить его в сторону от горизонта событий; однако ничего нельзя сделать, чтобы корабль (или даже луч света) оставался в этой области пространства неподвижным.
Этот эффект известен как “увлечение инерциальных систем отсчета” Лензе—Тирринга. Чтобы понять, почему это происходит, нам необходимо вспомнить принцип Маха, согласно которому любое тело во Вселенной вносит вклад в свойство инерции всех остальных тел. При нормальных условиях инерция тела определяется главным образом удаленными массами, но и близкие массы оказывают на нее некоторое (очень слабое) влияние. Следовательно, массивное вращающееся тело должно увлекать в круговое движение инерциальные системы в своей ближайшей окрестности. Этот эффект в принципе можно наблюдать с помощью маятника Фуко (маятника, свободно качающегося в “фиксированной” плоскости, относительно которой вращается Земля), установив его на одном из полюсов Земли и наблюдая, остается ли плоскость, в которой он колеблется, неподвижной относительно удаленных галактик или же она медленно поворачивается в направлении собственного вращения Земли. Эффект увлечения слишком мал, чтобы его можно было заметить с помощью современных приборов. Однако обусловленную этим эффектом прецессию орбиты спутника можно выделить среди других видов возмущений, хотя для того, чтобы вследствие этой прецессии плоскость орбиты спутника совершила один полный оборот вокруг Земли, потребуется почти 10 млн. лет.
В 1969 г. Роджер Пенроуз теоретически доказал, что из эргосферы черной дыры можно черпать энергию. Если какая-то частица, обладающая определенной энергией, попадет в эргосферу и разлетится на два осколка, один из которых имеет отрицательную энергию (и собственный момент импульса—спин, противоположный моменту импульса черной дыры), то этот осколок упадет в черную дыру, тогда как другой осколок (в соответствии с законом сохранения энергии и импульса) вылетит из эргосферы с энергией, превышающей первоначальную энергию всей частицы в целом. В принципе энергию вылетевшего осколка можно использовать для совершения полезной работы.
Падение частицы и вылет за пределы эргосферы одного из ее осколков приводят к уменьшению полной массы-энергии черной дыры, а многократное повторение этого процесса должно вызвать потерю значительной части массы-энергии черной дыры. Однако здесь есть определенные ограничения. Падение в черную дыру частиц со спином, противоположным ее собственному моменту импульса, вызывает замедление вращения черной дыры, и, как только вращение прекращается, дальнейшее извлечение энергии таким методом становится невозможным. Если мы начнем черпать энергию из черной дыры, вращающейся с максимальной допустимой скоростью (предельная керровская черная дыра), то к моменту ее полной остановки мы сможем извлечь 29% ее первоначальной массы-энергии, а это очень много: ядерные реакции, идущие в недрах звезд, далеко не столь эффективны — в них только около 1% массы вещества превращается в энергию. Рассмотренный Пенроузом процесс говорит о том, что потенциально вращающиеся черные дыры могут служить самыми мощными источниками энергии во Вселенной.
В 1971 г. профессор Кембриджского университета С. Хо-кинг доказал важную теорему, касающуюся возможности извлечения энергии из черных дыр, обобщив результат, полученный годом ранее Д. Кристодулу. Эта теорема о площади гласит, что площадь горизонта событий черной дыры не может уменьшаться: что бы ни происходило с черной дырой, “площадь ее поверхности” должна либо увеличиваться, либо оставаться неизменной. Площадь поверхности черной дыры пропорциональна квадрату ее массы (радиус черной дыры пропорционален ее массе, а площадь поверхности сферы пропорциональна квадрату радиуса). Если рассмотреть простой пример столкновения и “слипания” двух одина- ковых черных дыр, то в ходе этого процесса некоторая доля суммарной массы может быть утрачена—излучена в пространство в виде гравитационных волн. Максимально возможная потеря массы произойдет в том случае, когда площадь поверхности черной дыры, возникшей в результате столкновения, будет в точности равна суммарной площади поверхности первоначально сталкивающихся дыр, что и определяет верхний предел для освобождающейся в таком процессе энергии. Максимальное количество энергии, которая, согласно теории, может быть высвобождена при столкновении черных дыр, составляет 29% полной энергии двух столкнувшихся черных дыр. В действительности столкновение черных дыр в высшей степени маловероятно. Но даже если оно и произойдет, то вычисления показывают, что полный выход энергии будет значительно меньше указанного предела.
Как мы увидим ниже, черные дыры могут быть очень емкими источниками энергии. Даже невращающаяся черная дыра представляет собой достаточно глубокую гравитационную потенциальную яму, из которой энергия может высвобождаться гораздо более эффективно, чем при термоядерном синтезе. Например, падающие на черную дыру газово-пылевые облака в результате столкновения быстро ускоряющихся в них частиц должны нагреться до огромных температур, и, прежде чем исчезнуть за горизонтом событий, они будут излучать огромное количество энергии, главным образом в рентгеновском диапазоне. Итак, вещество, находящееся на некотором расстоянии от черной дыры, должно обладать значительным запасом потенциальной энергии; по мере падения вещества в черную дыру его потенциальная энергия превращается в кинетическую, которая, в свою очередь, частично превращается в тепловое или какое-либо другое излучение: так, кинетическая энергия падающего на землю камня рассеивается в почве в виде тепла, звуковых и ударных волн.
Хотя черные дыры абсолютно черны, т. е. из-под их горизонта событий излучение не выходит, их сильные гравитационные поля представляют собой самые мощные потенциальные источники энергии, которая может высвобождаться в процессе падения вещества под горизонт событий.
Внутри вращающейся черной дыры
Внутренность вращающейся (или заряженной) черной дыры существенно отличается от внутренности черной дыры Шварцшильда. Керровская сингулярность имеет форму кольца, и если изобразить ее на пространственно-временной диаграмме, то она в отличие от шварцшильдовской сингулярности будет направлена вертикально, т. е. параллельно направлению оси времени на диаграмме Пенроуза. Другими словами, сингулярность временноподобна. Это означает, что существует возможность проникнуть в черную дыру по пути, минующему центральную сингулярность и связанные с ней чудовищные гравитационные натяжения. Вообще говоря, чтобы падающее в керровскую черную дыру тело попало на сингулярность, его надо метко туда направить, так что разрушаются, попадая в кольцевую сингулярность, только те тела, которые движутся в экваториальной плоскости дыры.
На полной диаграмме Пенроуза, построенной для вращающейся черной дыры, видно, что такая дыра имеет два горизонта событий: внешний и расположенный ближе к сингулярности. Тело, попавшее под внешний горизонт, уже не может выйти наружу, поскольку, как мы знаем, свойства пространства-времени под этим горизонтом изменяются столь кардинальным образом, что движение в произвольном направлении полностью исключается. Под внутренним горизонтом событий свойства пространства-времени вновь изменяются, и падающее тело может двигаться здесь по мировой линии в сторону от сингулярности. Рисунок 35 позволяет нам проследить путь астронавта, падающего во вращающуюся черную дыру. В области, ограниченной внутренним горизонтом, астронавт способен изменить направление движения, включив двигатели своего корабля. Не превышая скорости света (т. е. двигаясь по линии, образующей с вертикалью угол менее 45°), он может отклониться от сингулярности, может даже двигаться в направлении от нее и в конечном счете оказаться в другом пространстве-времени. Упав в черную дыру в нашей Вселенной, астронавт уже не может вернуться в наш мир из той же дыры; значит, он должен выбраться из нее “где-то” еще — видимо, в другой вселенной.
Если вычертить диаграмму Пенроуза полностью, то мы увидим на ней бесконечное число вселенных прошлого и будущего. Влетая и вылетая из вращающихся черных дыр, наш бесстрашный астронавт до конца своей жизни будет путешествовать из одной вселенной в другую. Однако если изображенная на диаграмме физическая ситуация соответствует реальности, то астронавт может двигаться только в направлении “вселенной будущего”; упав в очередную черную дыру, он не сможет вернуться в свою собственную вселенную и встретиться там со своими современниками. Падение во вращающуюся черную дыру по-прежнему остается для астронавта путешествием в одном направлении, хотя и не обязательно ведет к его гибели. Аналогичным образом астронавты из других “миров прошлого” могут появляться в нашем мире, падая во вращающиеся черные дыры своих вселенных. Эти удивительные свойства решения Керра вызвали огромный интерес; представлялось, что керровская черная дыра открывает перед нами невероятные возможности.
В дальнейшем была высказана мысль, что, с одной стороны, “другие вселенные” могут быть нашей собственной Вселенной, а, с другой стороны, множество миров на диаграмме Пенроуза может быть связано путем, следуя по которому мы можем вернуться в нашу Вселенную, возможно в ее прошлое. Это обстоятельство открывает чудесную перспективу невероятных путешествий: практически мгновенно астронавт может перебраться в другую часть Вселенной; для этого ему достаточно совершить падение в надлежащим образом расположенную вращающуюся черную дыру. В частности, используя этот “черный ход”, можно попасть из пункта А в пункт В быстрее, чем в обычном пространстве от А до В дойдет луч света. Получается, что астронавт и впрямь ,мог бы, отправившись в путешествие, вернуться домой раньше своего отправления!
Как мы уже отмечали в гл. 4, такое развитие событий нарушило бы основной закон причинно-следственной связи: причина всегда предшествует следствию. Если бы эта связь оказалась нарушенной, то Вселенная была бы непредсказуемой и иррациональной.
С практической точки зрения путешествия в пространстве с помощью черных дыр вызывают одно существенное возражение: любой космический корабль, приблизившийся к горизонту событий дыры средней звездной массой, будет разорван на куски приливными силами. Но само по себе это не устраняет возможности обмена частицами и информацией через черные дыры с нарушением причинности. Если же говорить о сверхмассивных черных дырах, то здесь проблема приливных сил вообще не возникает: астронавты, проникшие внутрь дыры массой, скажем, в миллиард солнечных масс, могут путешествовать, не испытывая никаких неудобств.
Однако имеются гораздо более существенные возражения против использования вращающихся черных дыр в качестве “транспортного средства”. Последние теоретические исследования со все возрастающей определенностью свидетельствуют, что внутренность керровской вращающейся черной дыры (или заряженной черной дыры) ранее слишком идеализировалась: в реальной черной дыре, по-видимому, не может быть никаких пространственно-временных мостов. В модели Керра— Ньюмена черные дыры рассматривались как изолированные объекты в плоском (на бесконечности) мире, при этом не учитывалось действие находящегося поблизости вещества, а также возможные квантовые эффекты, влияние которых может быть весьма существенным. Так, в 1978 г. Н. Бирелл и •П. Девис показали, что квантовые эффекты не допускают существования пространственно-временного моста в заряженной черной дыре. В настоящее время делаются попытки применить аналогичные рассуждения и к вращающимся черным дырам. Вполне возможно, что в реальных вращающихся дырах сингулярность на самом деле будет не временноподоб-ной, а пространственноподобной—тогда падающий во вращающуюся черную дыру астронавт неминуемо погибнет в сингулярности, как и в черной дыре Шварцшильда.
Конечно, жаль потерять надежду на возможность удивительных путешествий с помощью черных дыр. Пока эта надежда еще существует, поскольку мы далеки от окончательного понимания того, чтб происходит внутри вращающейся черной дыры. Однако, как свидетельствуют последние исследования, такие путешествия вряд ли возможны даже в принципе.
|
|
 |
|
 | |
|
